1._ A continuación se muestra un programa que cuenta el número de apariciones de los números 0, 1, 2, 3 en una secuencia de enteros acabada en -1.

¿Que ocurrirá si tuviésemos que contar las apariciones de los cien primeros números enteros? ¿Deberíamos declarar cien contadores y escribir cien construcciones if para cada caso?
La respuesta, como era de esperar, se halla en el uso de vectores. Veámoslo en el siguiente programa:

Para entender con mayor claridad la practicidad y funcionalidad de los arreglos se muestra el siguiente ejemplo:
Suponiendo que tenemos una cantidad n de valores y queremos determinar cual de ellos es el mayor.
Suponiendo que no tenemos conocimientos del uso de arreglos, en caso de que se nos presentase el problema anterior tendríamos que hacer algo como lo que se muestra a continuación.
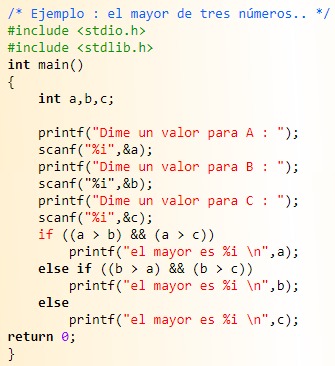
En este ejemplo se muestra un programa ineficiente, y además difícil de ampliar, para encontrar el mayor de tres números.
Como podemos ver para encontrar el mayor de más de tres números necesitaríamos reescribir el programa casi por completo. Pero si hacemos uso de arreglos podemos mejorar un poco esto, por lo menos facilitando la reutilización y mantenimiento del programa.
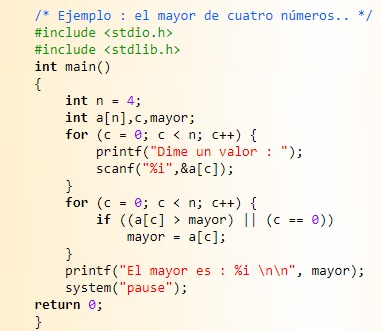
En este otro ejemplo se muestra otra solución al mismo problema de una mejor manera haciendo uso de las virtudes de los arreglos. Claro que esta tampoco es la solución mas optima. Pero a diferencia del primer ejemplo a este solo se le debe cambiar el valor de n para reutilizarlo con otras cantidades de números, o sea es un trabajo que es reutilizable y que en el futuro no tendremos que reescribir. El único problema en este pedacito de código es que para aumentar la cantidad de valores que soporta el programa se debe, todavía, modificar el código y recompilar.
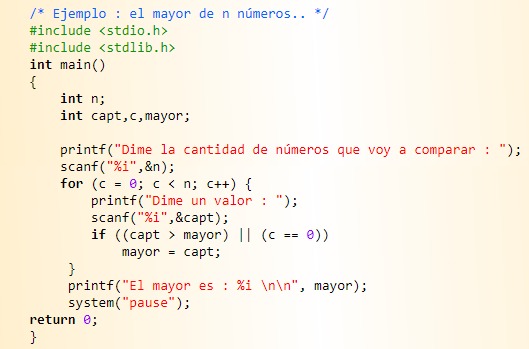
Esta es una manera todavía mas optima porque permite que el usuario decida que cantidad de números el va a introducir para comparar en tiempo de ejecución. Eso significa que no necesitamos recompilar el código.
2._ Vamos a crear un programa que lea un vector de 10 posiciones, luego determine si la quinta posición es positiva, si la primera posición es negativa y si la ultima posición es cero.(*)
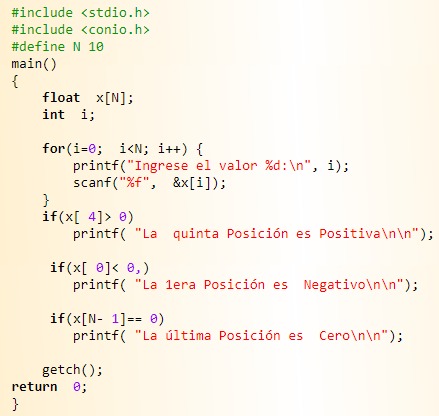
Cuando necesitamos manejar muchos datos, generalmente hay soluciones más efectivas que tener muchas variables. Por ejemplo, si hay que guardar 10 números, resultará incómodo usar 10 variables llamadas n1, n2, n3, n4, n5, n6, n7, n8, n9, n10; si se trata de 100 números, puede pasar de resultar incómodo a ser totalmente inviable. En esos casos, será más eficiente almacenar esos 100 datos "juntos", formando lo que se conoce como una "matriz", en vez de usar 100 variables distintas.
Normalmente, en una matriz podremos acceder individualmente a cada uno de sus elementos usando corchetes: el primer dato sería algo como "dato[1]".
Como primer contacto, se puede crear una matriz de 3 elementos, guardar datos en sus 3 posiciones y mostrar el primer dato y el tercero así:
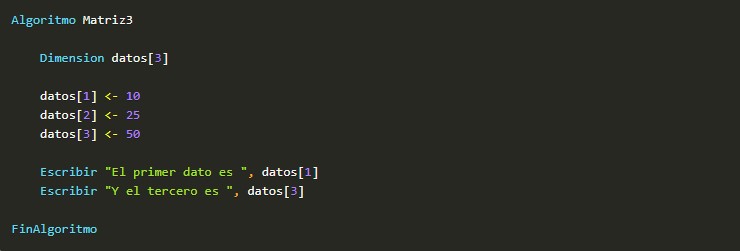
Como una matriz puede contener muchos datos, es frecuente recorrerlas de forma repetitiva, empleando una orden "para". Así un ejemplo que nos pida 6 datos y luego los muestre en orden contrario al que se han introducido podría ser:
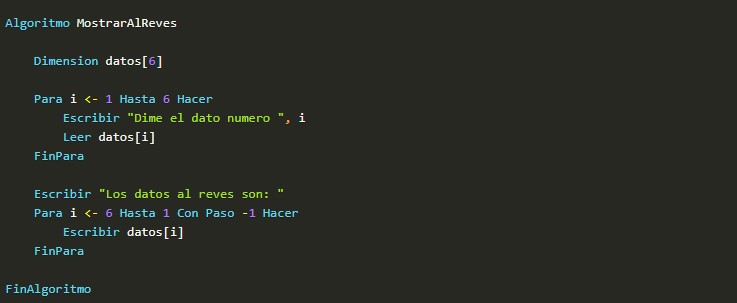
El resultado seria este:
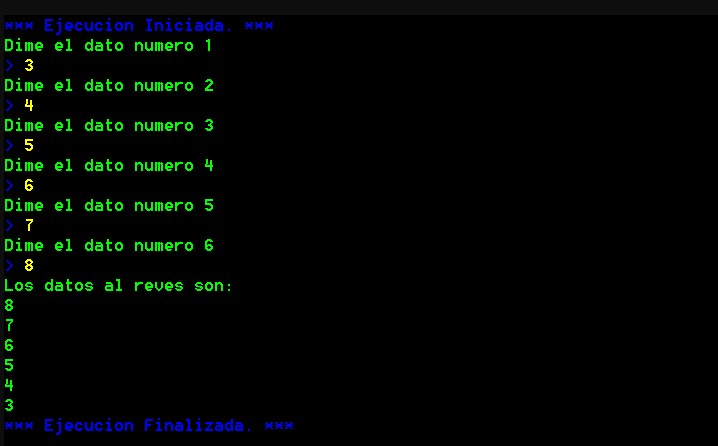
También se pueden crear arrays "de dos dimensiones" (por ejemplo, 3 filas y dos columnas), que se acercan más al concepto matemático de matriz:
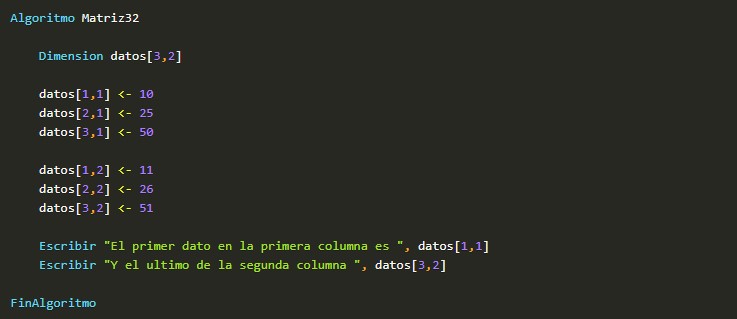
Si aun tienes dudas o quieres llegar a una mayor comprension e información, Te invitamos a ingresar a estos enlaces
Donde encontraras videos que te ayuden en una mejor comprension del tema